Recursion

Can you have a function or procedure call itself?

In computing, recursion relates to the use of recursive functions to solve problems. A recursive function is one that calls itself within its own definition. These can be a useful technique, and thinking through this will help reinforce the ideas of how functions work.

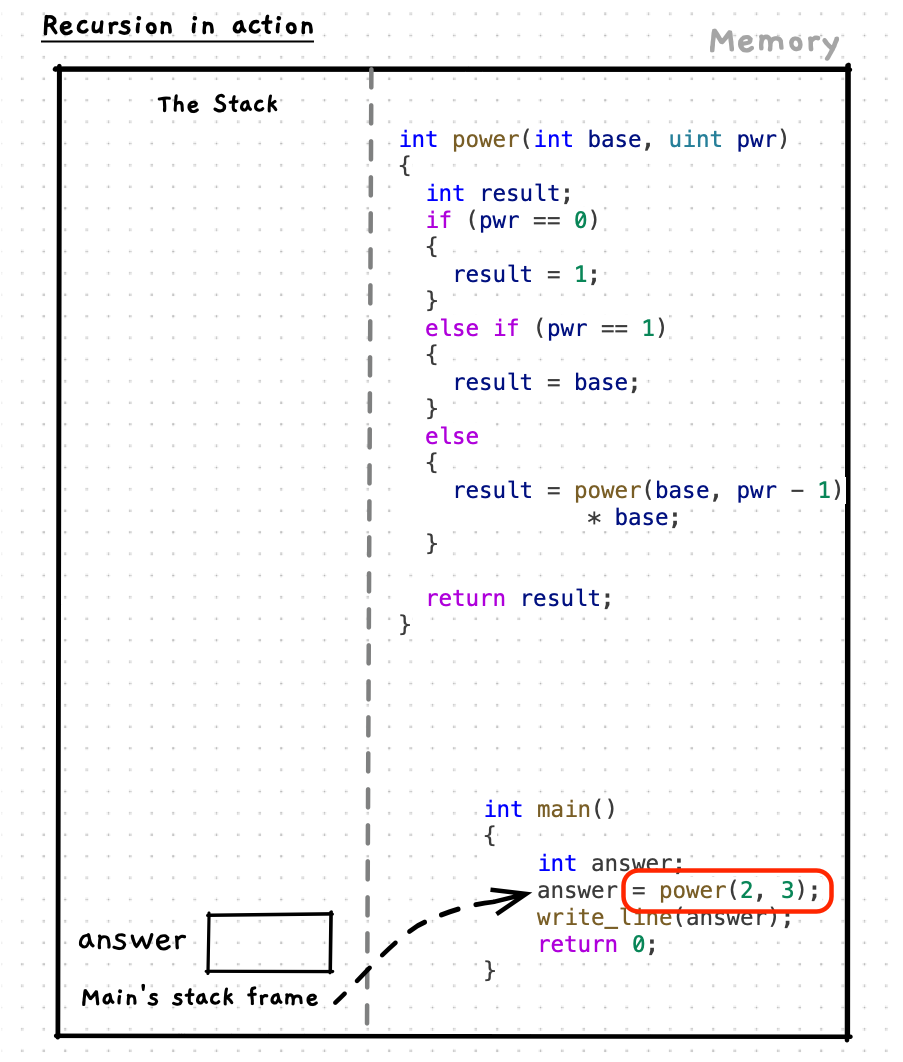
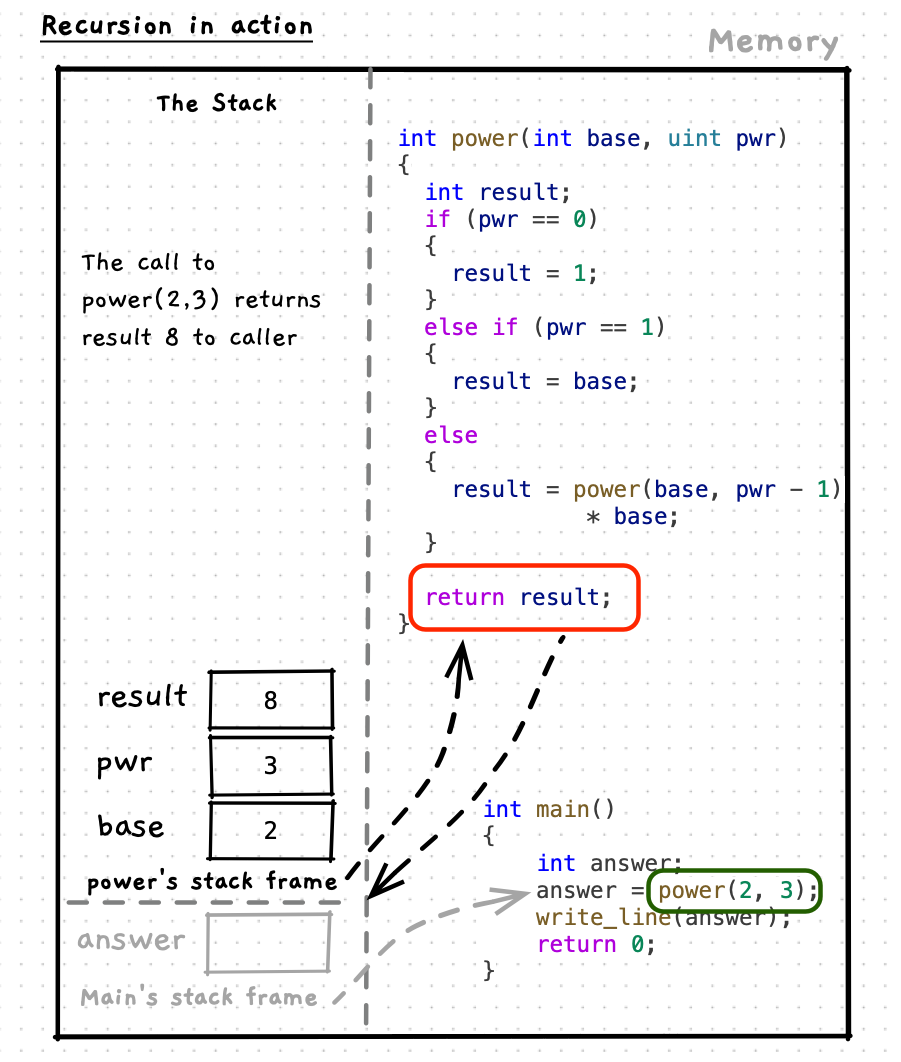
To start to understand recursive functions, let’s look at how it works mechanically. The following is a recursive definition of a power function. Notice, that we call the power function within its own body.

#include "splashkit.h"

/**
 * This function calculates the power of a base raised to an exponent.
 *
 * @param base the base number
 * @param pwr the exponent
 * @return int the result of base raised to the power of pwr
 */
int power(int base, uint pwr)
{
  int result;

  // Base case: if the power is 0, return 1
  // Base case: if the power is 1, return the base
  if (pwr == 0)
  {
    result = 1;
  }
  else if (pwr == 1)
  {
    result = base;
  }
  else
  {
    // Recursive case: multiply the base by the result of power with pwr - 1
    result = power(base, pwr - 1) * base;
  }

  return result;
}

int main()
{
  int answer;
  answer = power(2, 3);
  write_line(answer);
  return 0;
}

Recursion mechanics

How does this work?

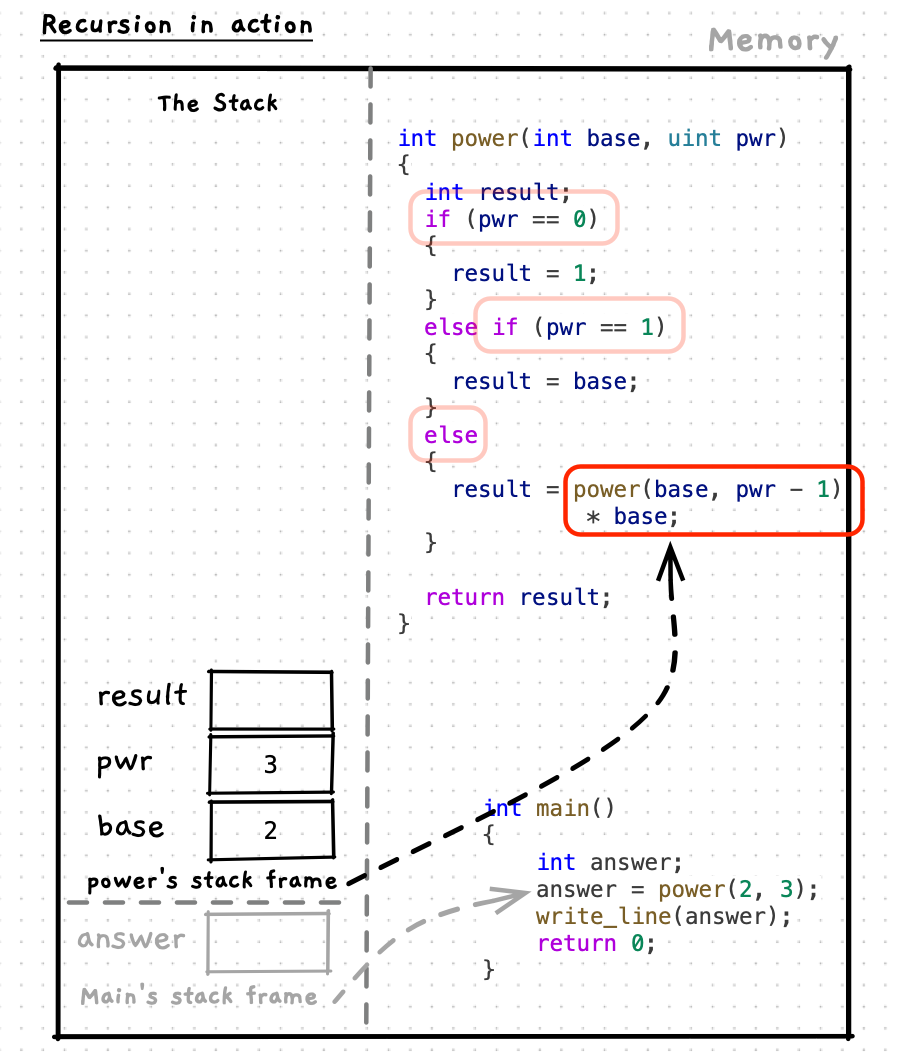
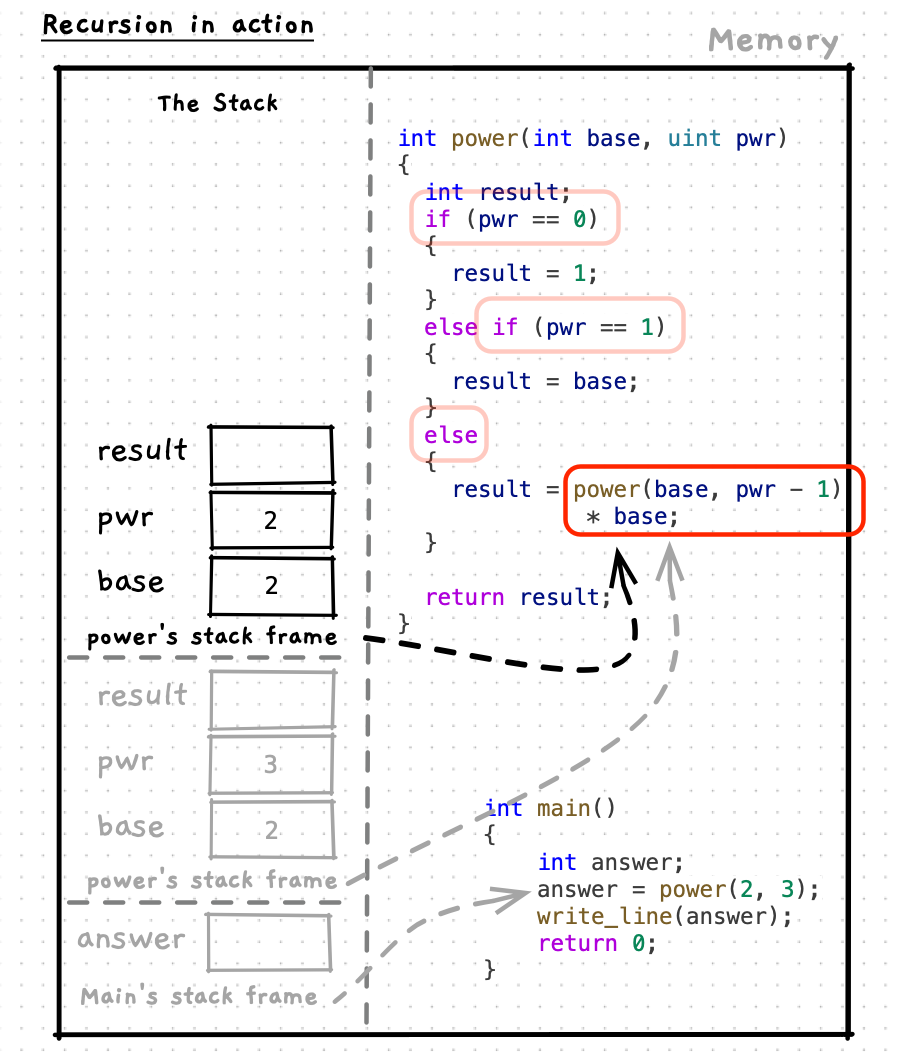
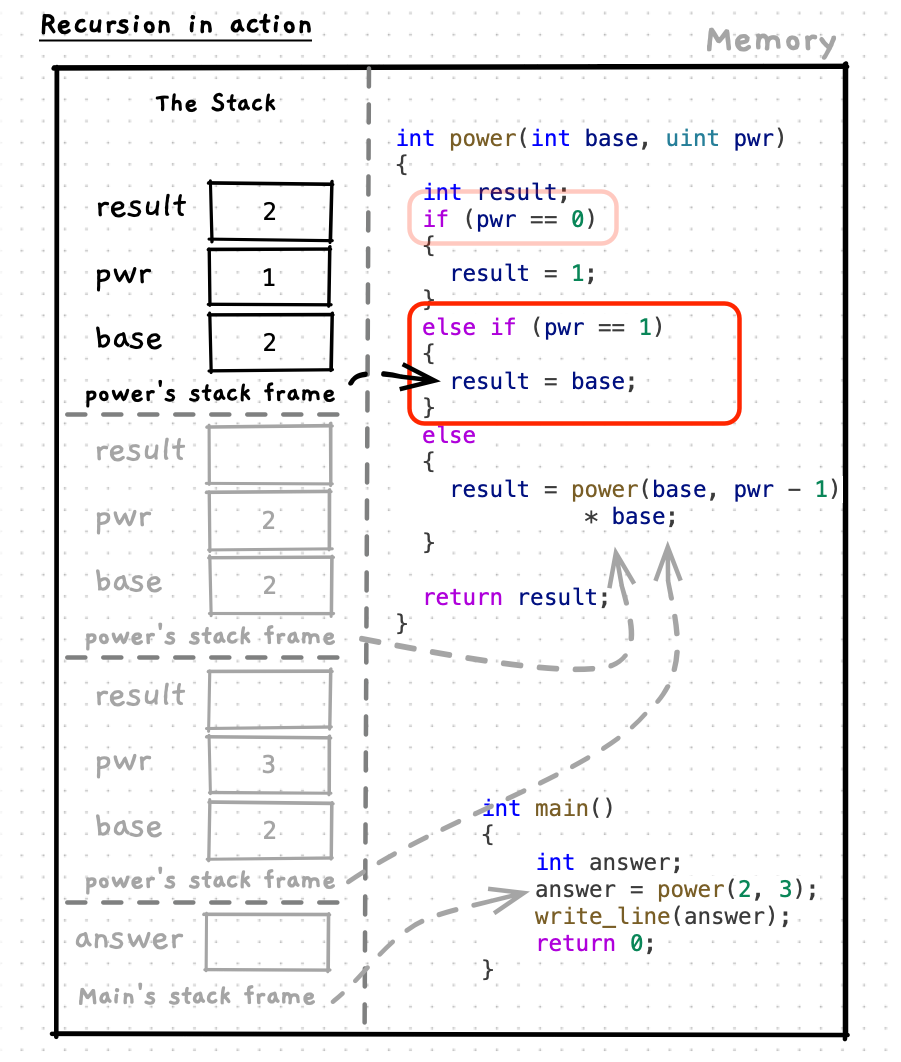
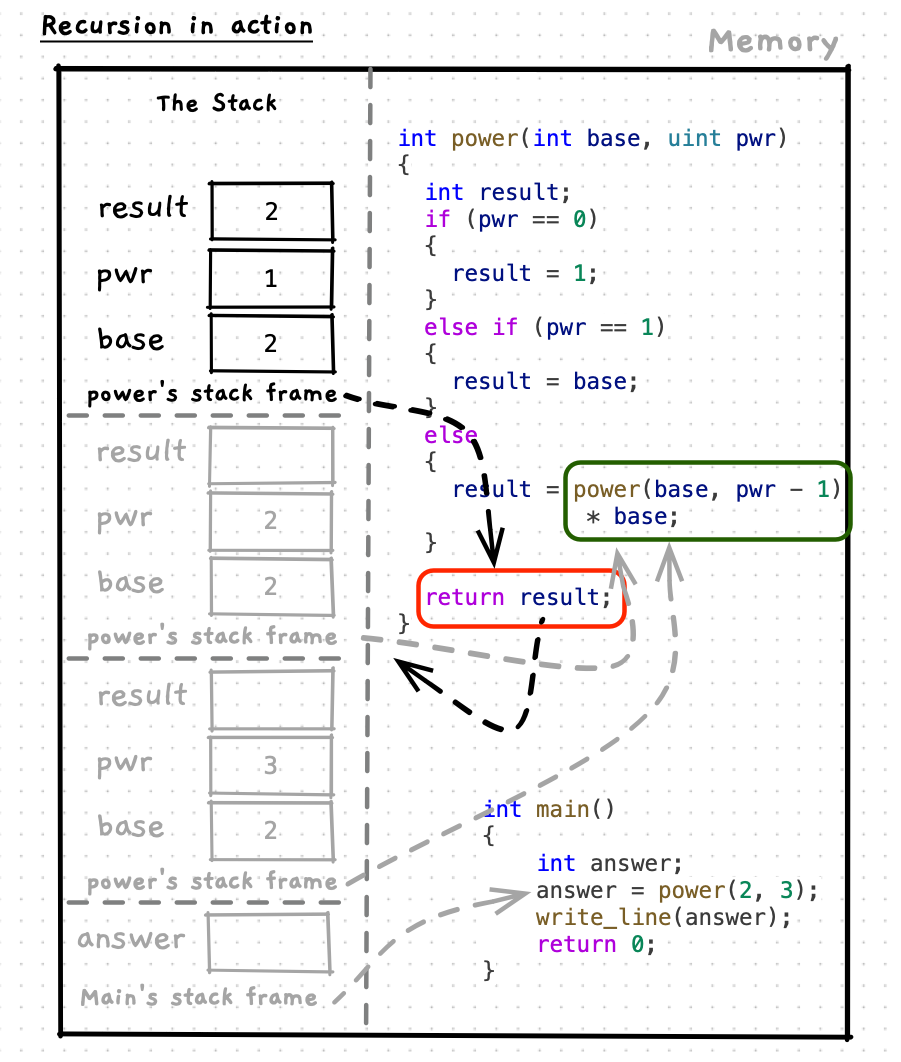
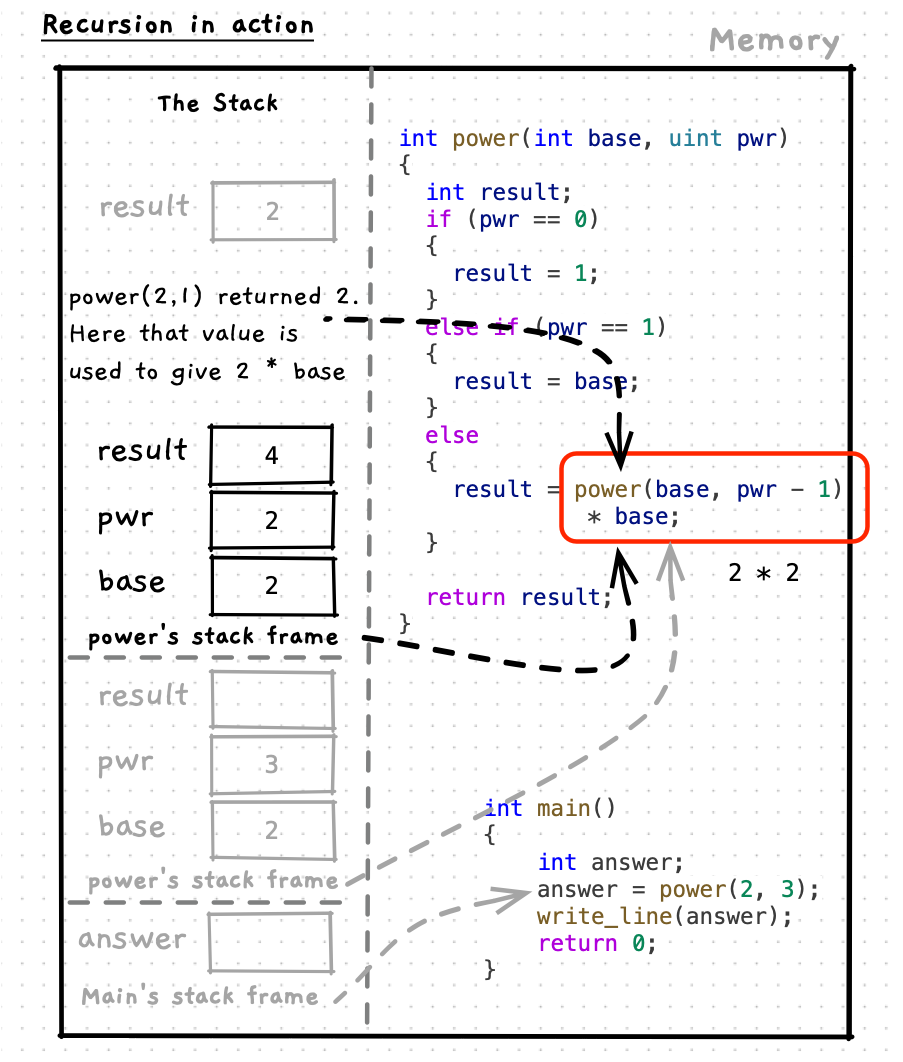
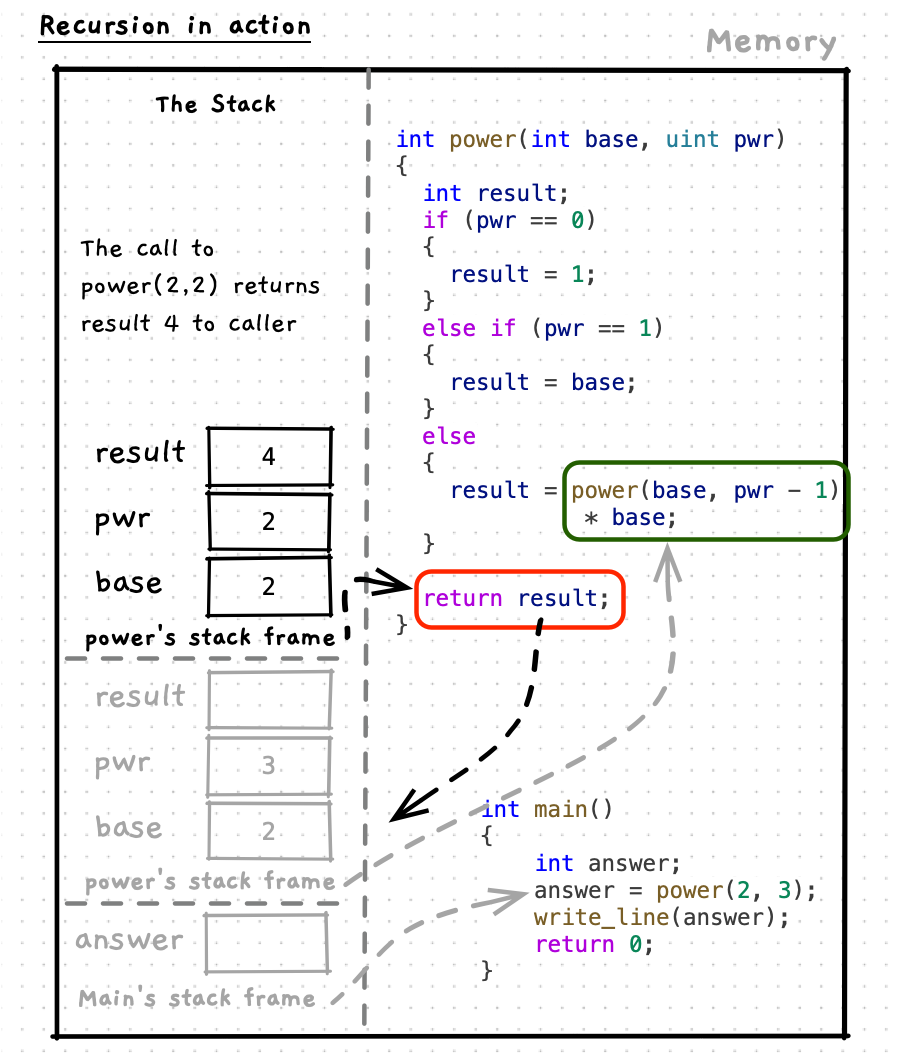
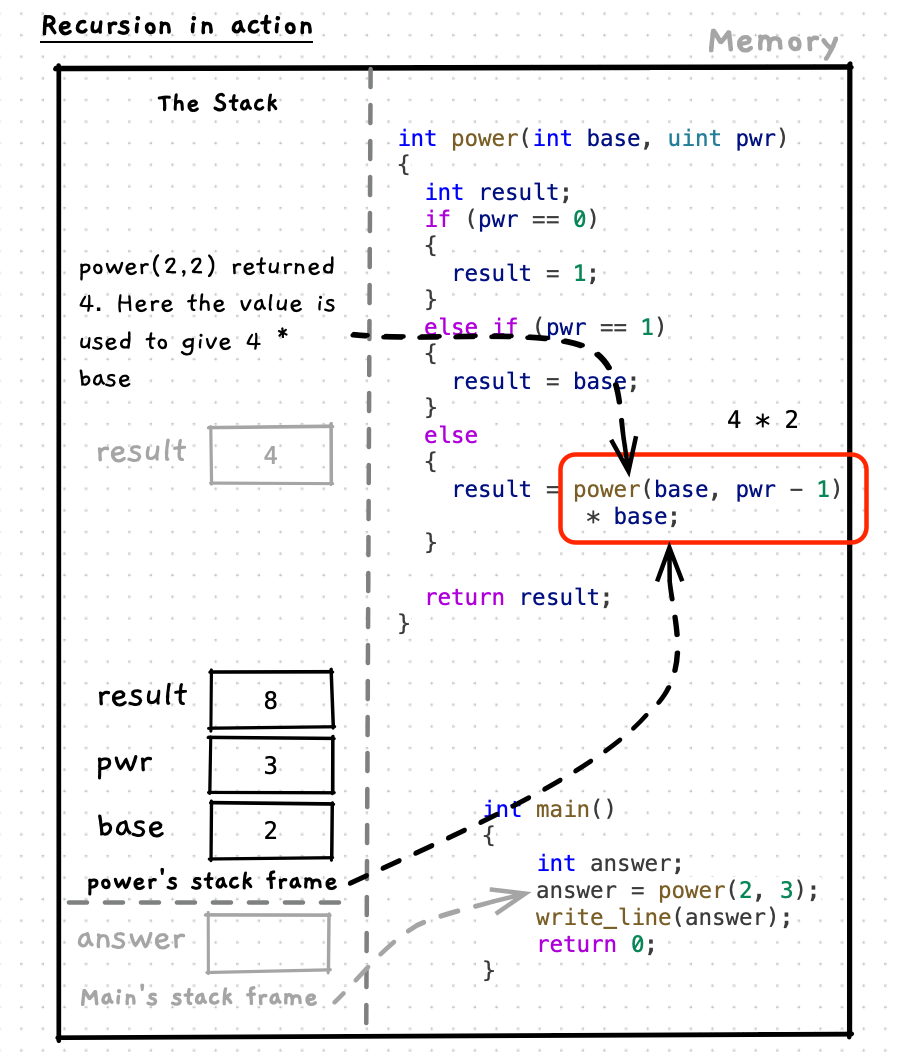
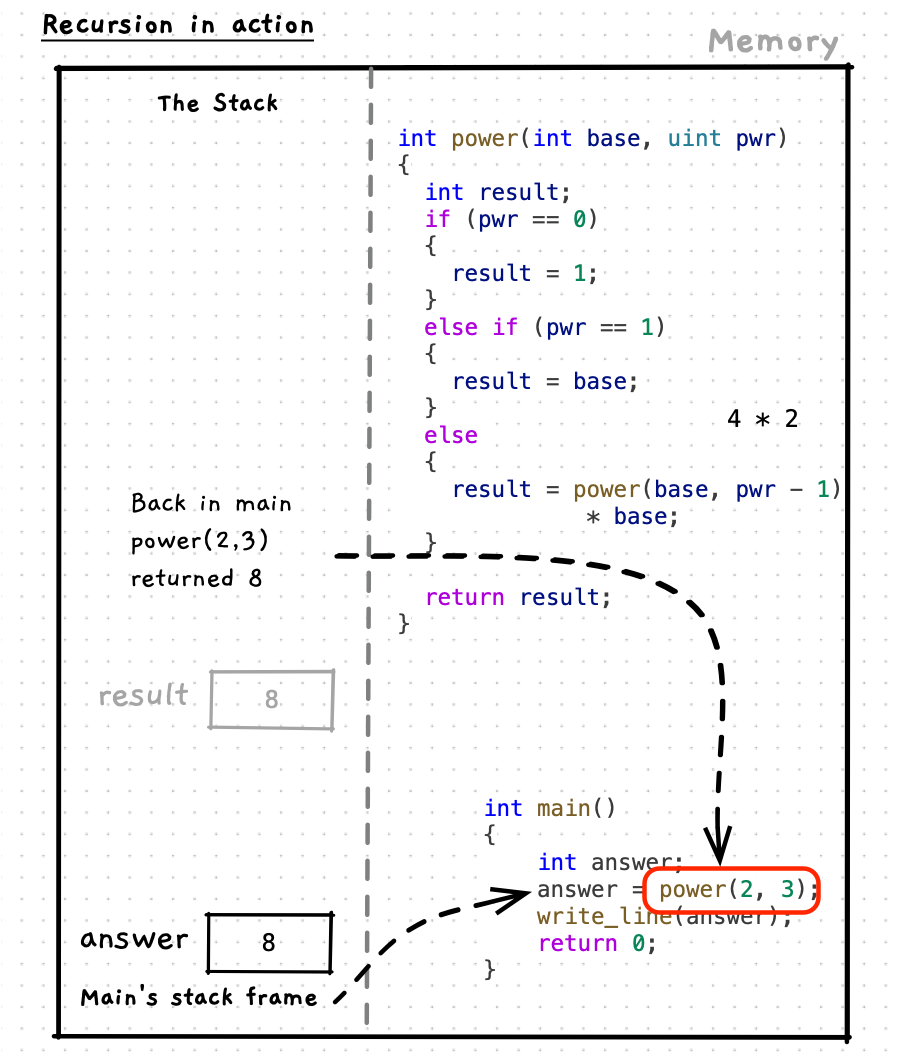
Let’s step through this code to see how it works. As you do this, notice how each function maintains its own state on the stack. This applies to any function/procedure call, but is particularly relevant when we think of recursion. Also pay attention to how each call to the function resolves its own answer - for example the call power(2, 2) calculates and returns the answer 4 as you would expect.

Program starts

• Main is on top of the stack
• answer is created in main
• We call power(2, 3) - starting our recursive function

 

What happens in power(2,3)

• Notice the stack frames - the call for power(2, 3) is on top
• pwr is not 0 or 1, so the else branch is taken
• We call power again - using the same base
• ... but we reduce the exponent (pwr) to be 1 less than the current pwr value
• This results in a new call, running power(2, 2)

 

What happens in power(2,2)

• Notice the stack frames - the call for power(2, 2) is on top
• The call for power(2, 3) is still on the stack, waiting for power(2, 2) to return
• pwr is not 0 or 1, so the else branch is taken (as with power(2, 3))
• We call power again - using the same base
• ... but we reduce the exponent (pwr) to be 1 less than the current pwr value
• This results in a new call, running power(2, 1)

 

What happens in power(2,1)

• Notice the stack frames - the call for power(2, 1) is on top
• The call for power(2, 2) is still on the stack, waiting for power(2, 1) to return
• The call for power(2, 3) is still on the stack, waiting for power(2, 2) to return
• pwr is not 0, so the first if branch is skipped
• pwr is 1 - so we take the second branch
• result is set to base (2)
• In a recursive function, a path that does not call the current function is called a base case

 

power(2,1) finishes and returns 2

• power(2, 1) now returns the value 2 to its caller
• This is returned to the previous function on the stack
• The call for power(2, 2) is waiting for power(2, 1) to return
• This will be where we return when the function completes - it will get the value 2
• The call for power(2, 3) is still on the stack, waiting for power(2, 2) to return

 

Back in power(2,2), we get the result and can proceed

• Notice the stack frames - the call for power(2, 2) is now on top
• It called power(2, 1) which returned 2
• We multiply this by the base, and store 4 in result
• The call for power(2, 3) is still on the stack, waiting for power(2, 2) to return

 

power(2,2) finishes and returns 4

• power(2, 2) now returns the value 4 to its caller
• This is returned to the previous function on the stack
• The call for power(2, 3) is waiting for power(2, 2) to return
• This will be where we return when the function completes - it will get the value 4

 

Back in power(2,3), we get the result and can proceed

• Notice the stack frames - the call for power(2, 3) is now on top
• It called power(2, 2) which returned 4
• We multiply this by the base, and store 8 in result
• main is still on the stack, waiting for power(2, 3) to return

 

power(2,3) finishes and returns 8

• power(2, 3) now returns the value 8 to its caller
• This is returned to the previous function on the stack
• main is waiting for power(2, 3) to return
• This will be where we return when the function completes - it will get the value 8

 

Back in main, 8 is returned by the call to power(2,3)

• main is now back on the top of the stack
• It called power(2, 3) which returned 8
• We store 8 in answer and proceed
• The recursive call has completed

 

Recursive thinking

Stepping through recursive functions can be tricky as you need to maintain the state of each function call yourself, in the same way that it is maintained on the stack when run in the computer. It is useful to do once to get an idea of how this works, but after that you need better tools to help you think through and design a recursive function.

How do you think about recursive functions?

Recursive functions need to have a known end-point, otherwise they would repeat infinitely (or until you run out of space for the stack). These end-points are known as base cases. In our power function we had two base cases: when pwr was 0 or 1. In these cases we do not need to call power again, instead we can return 1 when pwr is 0, and when pwr is 1 we can return base.

Tip

We could build this with a single base case where pwr is 0. Think through this yourself to make sure you can see the logic.

With the base cases identified, we can define the recursive case(s). This is where the function will call itself. The recursive case must move the state closer to the base case. In the example, power reduces the exponent value (in pwr) by 1. Moving it closer to the base cases of 0 and 1. This is where you need to isolate your thinking to focus only on the single calculation - using the parameters you have and at least one example to think through this.

For power, we can multiply the base by the power of the base raised to one lower exponent giving the recursive case the code result = base * power(base, pwr -1); (or result = power(base, pwr -1) * base;). That is the abstract, or general, case. Now we can validate this with some examples. For example, if we want to calculate 2⁴, we know that 2³ is 8, giving 8 * 2 = 16. You can then check this to validate the calculation. We can also test it next to the base case, to make sure that step works as well. In this case we can test 2² gives us 4. In this call we will have power(2, 2 - 1) * 2, we can simplify to power(2, 1) * 2. We also know that power(2,1) is a base case that will return the base, 2 in this case. So power(2, 1) * 2 can be simplified to 2 * 2, giving us the expected result of 4.

If you can see how each recursive case is moving toward a base case, and you can satisfy yourself that a single recursive call works, then you should have a valid design for your recursive call.

Notice in this case that we declared pwr as an unsigned integer. This ensures that we do not get negative values for the exponent. If you used an integer, you would need an additional base case to handle values that we less than 0. What would happen if we used an integer and called power(2, -3). Would the current logic move it toward the base case? Test this out for yourself.

Recursion - Why, When, and How

Can’t I just use a while loop?

This is a good question. The following code shows how the power function implemented using a loop. This is relatively straightforward. If you think about it, you will also see that this is much more efficient. The loop does not result in repeated function calls - each of which need to be added to the stack. So, when possible you should just use a loop to achieve your results if you can.

/**
 * This function calculates the power of a base raised to an exponent.
 *
 * @param base the base number
 * @param pwr the exponent
 * @return int the result of base raised to the power of pwr
 */
int power(int base, uint pwr)
{
  int result = 1;

  while ( pwr > 0 )
  {
    result *= base;
    pwr--;
  }

  return result;
}

Why touch on recursion?

Being able to think recursively is important, as this can be useful in different ways as you study additional programming techniques. This also helps encourage you to think through each function as an isolated entity. With recursion, thinking through the recursive steps helps encourage you to be able to rely upon other function calls to take care of their responsibilities, even when that function is the one you are currently writing.

Are there some other classic recursive problems

There are a few classic problems that you often encounter when exploring recursion for the first time. We will look at how you can use recursion to create the Fibonacci sequence and use it to solve the Towers of Hanoi.